pdf code

Denoising Diffusion Probabilistic Models

这篇paper是diffusion model在生成模型中的应用。这篇文章有一个推导公式比较细致，讲解比较清晰的博客.

Diffusion Model 在生成模型中的特点

该博客中有如此一图，大致总结了当前生成模型的四大类别。对抗网络, VAE, flow-based model, 以及本文的扩散模型。

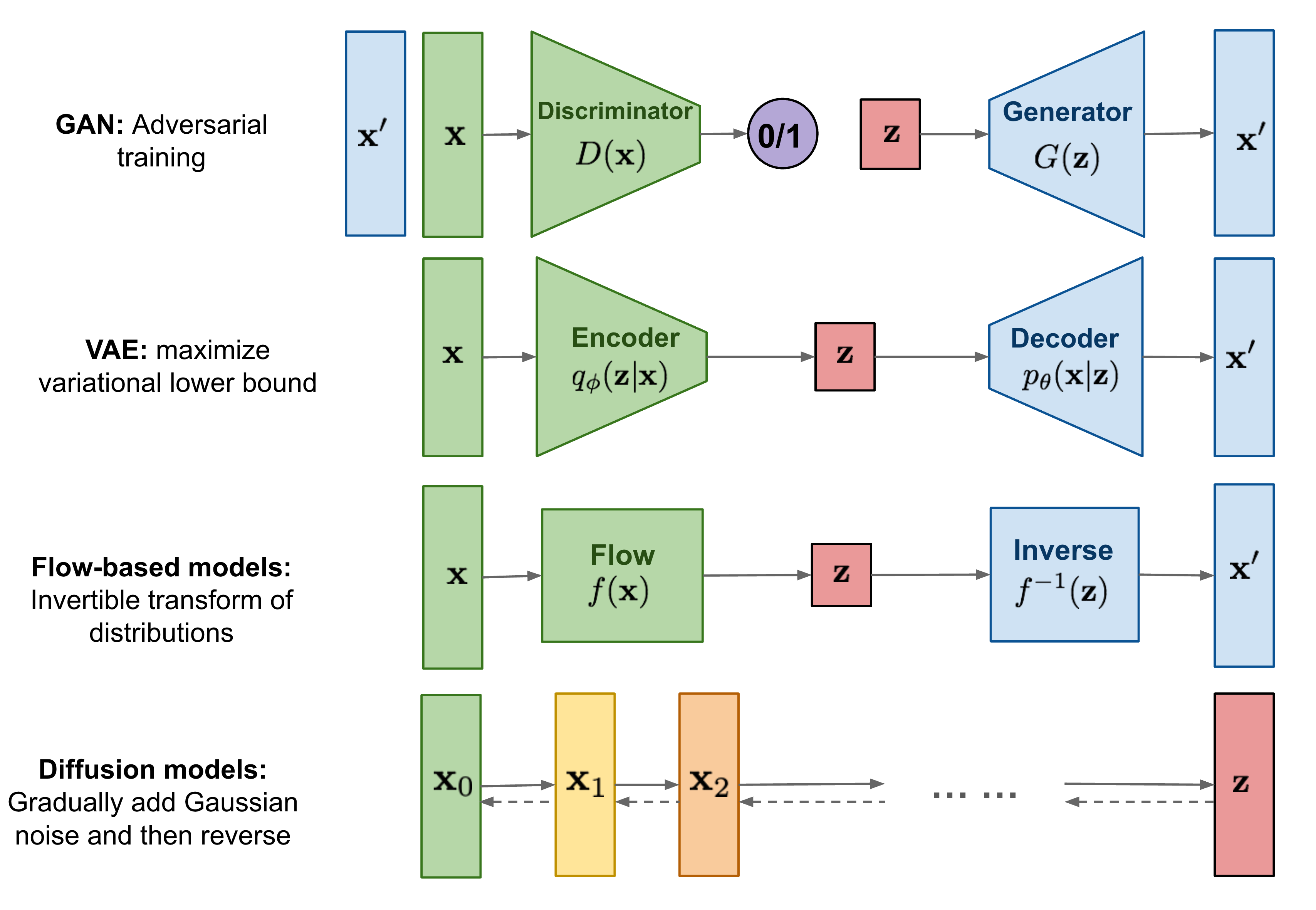
这几种方式的对比来看，VAE和Flow Model可以快速地采样出种类范围比较广的样本。GAN可以快速采样出质量高的样本，而Diffsion则采样速度慢，但是采样范围种类广且质量很高。

Denoising Diffusion Model 主要工作流与组件分类

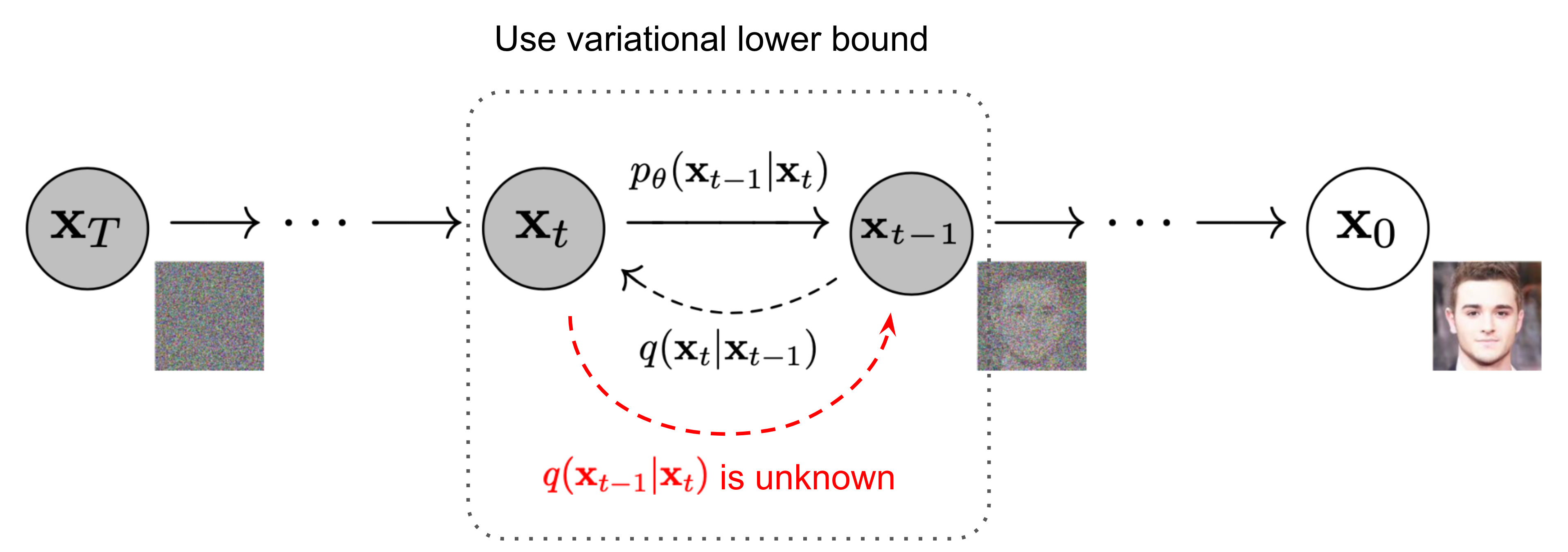Diffusion 操作上表达的是对图片逐步增加高斯噪声，最终把图片完全corrupt 成噪音的过程，而反向地，从噪音中还原出图片地pattern则是生成的过程。

数学上来说对图片/数据逐步增加高斯噪声的过程被设计成一个马尔可夫链，每一个时刻的状态只由上一个时刻的均值以及额外的噪声影响。概率地写出公式 $q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t \mathbf{I})$, 白话而言就是把前一个时刻的图像/数据/分布scale down, 再与一个额外的高斯分布加和。

反向的时候我们已知$x_T$,需要逐步估计第$T$步的噪音$z_t$，然后让数据"减去"这个噪音。本文提出的就是用神经网络，输入$x_T$和$T$时刻的time_encoding, 估计这个分辨率与原图一样的噪音,并逐步去除噪音得到原图。因而称为"Denoising Diffusion Model".

因而在功能模组上，这类模型分为一下几个部分，不同的文章会有不同的假设以及选择，后面会再数学与代码上给出实例.

• 前向采样,计算从图片到第$T$时刻被corrupt的状态. 这里的主要变量在于采样时间可变，且$\beta(t)$关于时间的函数，称为noise scheduler是可控制的，如线性增加噪声等方案。
• 噪声估计网络$\Theta$, 输入$x_t$时刻图片以及time encoding输出同分辨率噪声$z_t$, 以UNet为主架构，配合Attention等模块选择 (比如后来一些加入语言或外部信息的生成模型多使用attention).
• 损失函数，如何训练噪声估计(图片估计)网络，可以有很强的概率学支撑，也可以像本文最后的baseline implementation一样简单暴力。
• 采样推理，所谓的"减去噪音"步骤，这里可以有更严谨的推导计算得到更准确的数值。

前向采样

如果输入图片也是高斯分布，高斯分布与高斯分布的叠加是闭式的高斯，用递推的公式计算采样的推理过程，可以很快发现我们不需要多步迭代来实现加噪音采样，而是可以根据noise scheduler以及随机数生成器直接得到任意时间点的噪音和图像数据。 令$\alpha_t = 1 - \beta_t$, $\bar{\alpha}_{t}=\prod_{i=1}^{T} \alpha_{i}$, $z_t$是代码从高斯分布中采样的噪声。

$$\begin{aligned} x_t &= \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} z_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-1} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{z}_{t-2} \\ &= \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t} \bar{z_0} \end{aligned}$$

注意两个高斯噪声方差为$\sigma^2_1, \sigma^2_2$的$z$的融合，得到的是一个方差为$\sigma_1^2 + \sigma^2_2$的高斯分布。所以上文的计算实际上是 方差为$1-\alpha_t$的高斯分布和$\alpha_t * (1-\alpha_{t-1})$的高斯分布的融合，得到的就是方差为$1 - \alpha_t\alpha_{t-1}$的高斯分布，累积结果同样。至此，我们可以根据原数据$x_0$, 噪声规划器得到的$\bar\alpha_t$, 以及采样的高斯噪声得到任意时刻的图片$x_t$

采样推理

作者指出，在已知(conditioned on) $x_t, x_0$时，反向概率也符合一个高斯分布

$$q(x_{t-1} | x_{t}, x_0) = \mathcal{N}(x_{t-1}; \tilde\mu(x_t, x_0), \tilde\beta_t \mathbf{I})$$

由于前向的概率分布是已知的，这里的后验分布就用贝叶斯公式转换为前向 (分子是$x_t, x_{t-1}$的乘积概率，更改条件概率的条件 conditioned on $x_{t-1}$, 可将全部变为前向)；并重点关注概率分布函数的指数部分, 然后把其中的$x_{t-1}$提出来。 $$\begin{aligned} q(x_{t-1} | x_t, x_0) &= q(x_t | x_{t-1}, x_0) \frac{q(x_{t-1} | x_0)}{q(x_t | x_0)} = q(x_t | x_{t-1}) \frac{q(x_{t-1} | x_0)}{q(x_t | x_0)} \\ & \propto \text{exp} (-\frac{1}{2} (\frac{(x_t - \sqrt{\alpha_t} x_{t-1})^2}{1-\alpha_t} + \frac{(x_{t-1} - \sqrt{\bar\alpha_{t-1}}x_0)^2}{1 - \bar\alpha_{t-1}} - \frac{(x_t - \sqrt{\bar\alpha_t}x_0)^2}{1 - \bar\alpha_t})) \\ &=\text{exp}(-\frac{1}{2}[ (\frac{\alpha_t}{1 - \alpha_t} + \frac{1}{1-\bar\alpha_{t-1}}) x_{t-1}^2 - \\ &(\frac{2\sqrt{\alpha_t} x_t}{1 - \alpha_t}+ \frac{2\sqrt{\bar\alpha_{t-1}}x_0}{1 - \bar\alpha_{t-1}} )x_{t-1} + C(x_t, x_0) ] ) \end{aligned}$$ 通分并凑平方，找出$x_{t-1}$的方差和均值. 由$Ax^2 - 2Bx = \frac{(x - B/A)^2}{1/A}$, 其中$A = \frac{\alpha_t}{1 - \alpha_t} + \frac{1}{1-\bar\alpha_{t-1}} = \frac{1 - \bar\alpha_t}{\beta_t (1 - \bar\alpha_{t-1})}$

方差 $\sigma^2 = 1 / A = \frac{\beta_t (1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}$.

把$x_0 = \frac{x_t - \sqrt{1 - \bar\alpha_t} \bar z_0}{\sqrt{\bar\alpha_t}}$ 代入$B$中，

$$\begin{aligned} B &= \frac{\sqrt{\alpha_t}}{1 - \alpha_t} x_t + \frac{x_t}{(1-\bar\alpha_{t-1})\sqrt{\alpha_t}} - \frac{\sqrt{1-\bar\alpha_t}z_0}{(1-\bar\alpha_{t-1})\sqrt{\alpha_t}} \\ &= \frac{(1-\bar\alpha_t)x_t}{(1-\alpha_t)(1-\bar\alpha_{t-1})\sqrt{\alpha_t}} - \frac{\sqrt{1-\bar\alpha_t}z_0}{(1-\bar\alpha_{t-1})\sqrt{\alpha_t}} \end{aligned}$$ 均值 $$\mu = B * 1/A = \frac{1}{\sqrt{\alpha_t}} x_t - \frac{1 - \alpha_t}{\sqrt{\alpha_t} \sqrt{1 - \bar\alpha_t}} z_t$$ 从此可计算出$q(x_{t-1}|x_t, x_0)$是一个仅与$x_t, z_t$有关的，以$\mu, \sigma^2$为特征的高斯分布。这个均值的计算也可以直观地理解为增强输入数据并减去一个估计的噪声$z_t$, 就是前向采样的一个逆运算。这个式子也说明了，为什么我们说可以通过估计噪声几乎等价于直接估计$x_{t-1}$

损失函数

直观的设计是说根据前文，计算重建每一个时间$t$的图像，比较反向和正向的图片的相似度作为损失函数，本文则进一步简化这个结果，最终采用的是一个$L_2$函数，比较预测出来的噪声和实际的噪声的相似性。如果能通过被干扰的图片准确地预测噪声，显然我们就能反推得到原来的输入图片。因而这个损失是直观合理的。

作者进一步从数学角度有分析,思路与VAE很接近。首先明确需要优化问题是$\argmax_\theta{p_\theta(x_0)}$, 也就是选择参数$\theta$， 最大化网络预测的映射函数$p_\theta$在数据集数据$x_0$中概率。

模仿VAE的推理，可以计算得到

$$D_{KL}(q(x_{T:1} | x_0) || p_\theta(x_{T:1} | x_0)) = \log{p(x_0)} + \mathbb{E}_{x_{T:1} \sim q(x_{T:1} | x_0)}[\log\frac{q(x_{T:1} | x_0)}{p(x_{T:0})}] > 0$$ $$\log{p(x_0)} > -\mathbb{E}_{x_{T:1} \sim q(x_{T:1} | x_0)}[\log\frac{q(x_{T:1} | x_0)}{p(x_{T:0})}]$$ 从而确定了$\log p(x_0)$ 的下限(ELBO),注意右项这里$q$是前推函数容易表达，也就是高斯，而$p$是后推条件函数容易表达，也就是网络的预测(噪声).

$$\begin{aligned} L_{\mathrm{VLB}} &=\mathbb{E}_{q\left(\mathbf{x}_{0: T}\right)}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0: T}\right)}\right] \\ &=\mathbb{E}_{q}\left[\log \frac{\prod_{t=1}^{T} q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)}{p_{\theta}\left(\mathbf{x}_{T}\right) \prod_{t=1}^{T} p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}\right] \\ &=\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=1}^{T} \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}\right] \\ &=\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right] \\ &=\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \left(\frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)} \cdot \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{0}\right)}\right)+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right] \\ &=\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{0}\right)}+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right] \\ &=\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}+\log \frac{q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right] \\ &=\mathbb{E}_{q}\left[\log \frac{q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{T}\right)}+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}-\log p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)\right] \\ &=\mathbb{E}_{q}\left[D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right) \| p_{\theta}\left(\mathbf{x}_{T}\right)\right)+\sum^{\mathrm{T}}_{t=2} D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right) \| p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\right)-\log p_{\theta}\left(\mathbf{x}_{0} | x_1\right)\right]\end{aligned}$$

上文第一项与$\theta$无关，因为$p(x_T)$就是噪声，正太高斯分布。最后一项根据的是最后一步的逆推公式做。而中间部分就是两个高斯之间的相似度(KL距离)，

高斯之间的相似度严格来说应该如下: $<script type="math/tex; mode=display">\begin{aligned} K L(p, q) &=-\int p(x) \log q(x) d x+\int p(x) \log p(x) d x \\ &=\frac{1}{2} \log \left(2 \pi \sigma_{2}^{2}\right)+\frac{\sigma_{1}^{2}+\left(\mu_{1}-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}-\frac{1}{2}\left(1+\log 2 \pi \sigma_{1}^{2}\right) \\ &=\log \frac{\sigma_{2}}{\sigma_{1}}+\frac{\sigma_{1}^{2}+\left(\mu_{1}-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}-\frac{1}{2} \end{aligned}$

但是可以通过训练噪音或者重建图片的相似性直接绕过这个损失函数的选择。不同点只是在参数的权重上，因而不是重点。但这个推理过程说明了此前简单损失的充分性。

youtube 上的上手视频